Jeg mener det er viktig at brukere av IT lærer seg å bruke det som et naturlig hjelpemiddel og verktøy til anvendelser det er godt egnet til.
To gode anvendelser er
Kontroll av vanlige pensumoppgaver når man arbeider individuelt hjemme er en viktig aktivitet!
|
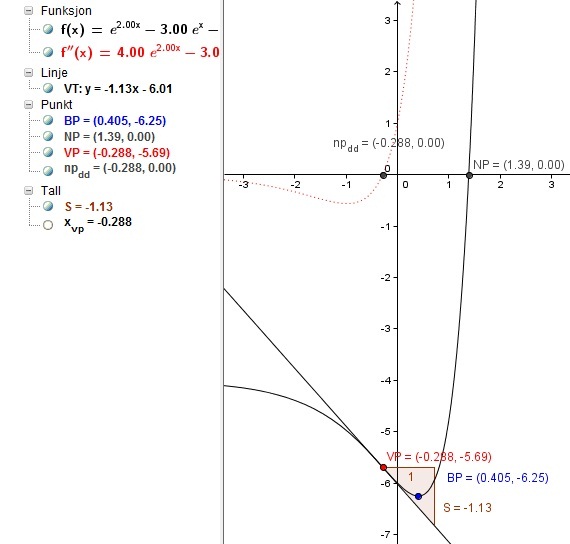
Kontroll med GeoGebra vil gi følgende modell:

Kommando: Kommentar: f(x)=exp(2*x)-3*exp(x)-4 Legger inn funksjonen i GeoGebra.
(Kan også gjøre det slik: f(x) = e^(2 x)-3 e^x-4)Nullpunk til f(x): NP=Nullpunkt[f,1,2] GeoGebra finner nullpunktet i intervallet <1,2,> Ekstremalpunkter til f(x): BP=Ekstremalpunkt[f,0,1] Finner bunnpunktet BP i intervallet <0,1> f''(x) GeoGebra finner den dobbeltderiverte av f(x) np_{dd}=Nullpunkt[f'',-1,0] GeoGebra finner nullpunktet i intervallet <-1,0> for f''(x).
Legg merke til at vi må bruke krøllparenteser fordi det blir
mer enn et tegn i indekseringen av navnet npdd:
- np_{dd}
x_{vp}=x(np_{dd}) x-koordinaten til vendepunktet er x-verdien til nullpunktet til
den dobbelt-deriverte.VP=( x_{vp} , f( x_{vp} ) ) Toppunktet har samme x-koordinat som nullpunktet til f''(x). Vendetangent: VT=Tangent[VP,f] GeoGebra finner vendetangenten til vendepunktet VP på f(x). S=Stigning[VT] Stigningstallet til vendetangenten.
(Som også sees av ligningen for vendetangenten i Algebravinduet.)